Turkey Dinners and Cache Conscious Programming

Have you ever tried baking a pizza in an oven at an eighth the recommended temperature? The pizza will in fact never be fully cooked, never achieving a high enough temperature to melt the cheese, crisp the bread, etc.

In many ways, crafting programs are similar to baking a pizza. It requires some finesse and skill to make a pizza (alright maybe not that much skill, but go with it), similarly you need to have some finesse and skill to build a program. One particular skill every programmer should attempt to expand upon is cache optimization, since it is required for parallel programming and can significantly affect the speed of a program.

A Turkey Dinner

Back to the kitchen/food analogy, you can think of a cache as the food you have on the kitchen table, your working memory, RAM (random access memory) as the kitchen and your hard drive as the grocery store. In essence a cache is where your data is stored for processor use. A cache allows a processor to access the a particular file within a few clock cycle, most modern CPU’s (central processing units) consist of several caches of varying size.

For example, consider you have friends over for a turkey dinner, but only have enough room on the table for the potatoes and turkey. This means that you only have access to the potatoes and turkey without having to get up. You keep the rest of the food, stuffing, rolls, vegetables, pie in the kitchen, and consider this your RAM. The food is close enough that you really don’t worry, but far enough away that you really don’t want to get up too often. You therefore ask everyone to grab as much turkey as they want before switching out the turkey tray with the vegetables. Further, it may make more sense to keep the pie furthest away in the kitchen since it’s the last thing you will eat. It wouldn’t make sense to put the pie on the table before the turkey has been served (at least not in my house). This is nearly identical to the way in which you want to program.

For comparison purposes, here are the times for a processor to access each given cache for the Intel I7-965[1] in a random order:

• L1D Cache – 32Kb – Each processor has its own –  the smallest cache directly next to the processor takes 4 clock cycles to retrieve data.
• L2 Cache – 256Kb – Each processor has its own – The second smallest cache, used to load data into the L1D cache, takes 12 clock cycles to retrieve data.
• L3 Cache – 8Mb – Shared amongst processors – shared between all caches requires 40 clock cycles to retrieve data.
• RAM – 12 Gb – Shared amongst processors – 62.5 ns or at 3.2 Ghz =>  0.0000000625(sec) * 3200000000(hz) = 200 clock cycles on average.
• Hard Disks – Varies wildly, but according to Quora if we attempted to load a gigabyte from disk (1 Gb = 1000 Mb) it would take ~0.078s given DDR3 (the fastest RAM on the market at the moment). This means 0.078s * 3200000000(hz) = 249 600 000 clock cycles.

In contrast, here are the times for a processor to access each given cache for the Intel I7-965[1] in a sequential order (same size and characteristics as above):

• L1D Cache – 4 clock cycles to retrieve data.
• L2 Cache –  12 clock cycles to retrieve data.
• L3 Cache – 15 clock cycles to retrieve data.
• RAM – 7.2 ns or 23.04 clock cycles on average.
• Hard Disks – still 249 600 000 clock cycles.

This implies that the hardware will actually access data quicker if it is accessed sequentially, meaning the hardware attempts to do the same thing as the turkey dinner example, grab what you need in order. The term for this is is called prefetching, meaning that your hardware preloads what it expects you to access next, similar to presenting on the vegetables or turkey previous to the pie in the example.

How to be Cache Conscious

Knowing a little bit about your cache can make a big difference, take for example the three following code snippets:

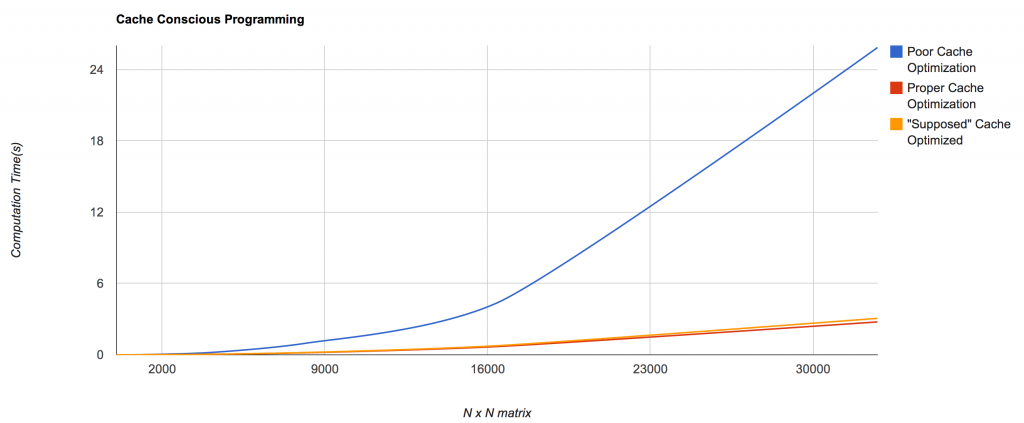
The following is a graph of the previous functions given a matrix of size N x N (horizontal) and the vertical axis representing the time it took (in seconds) for the program to complete. The graphs and data were obtained with a 2.3 GHz Intel Core i7, 8Gb ram, compiled with g++4.2:

As you can see the “poor cache optimization” has by far the worst performance. Yet, if you review the code snippet for the “poor cache optimization” the only difference between that and the “proper cache optimization” function would be that the order of the for loops have been flipped. This means that the poor_cache_opt only performs poorly because of the order in which the array is accessed, more the the point:

In the poor case, the inner loop iterates through the rows of the matrix. Meaning each time y increases, it progresses along a column, as opposed to the proper case:

In which the inner loop iterates through the columns as opposed to the rows. Meaning that each time y iterates it progresses along a row.

The difference between the two functions stems from the way in which memory is stored and brought into the cache. In most (nearly all) architectures arrays are stored as continuous pieces of memory. That is to say, they are stored in memory in order and as consecutive chunks, as opposed to having memory everywhere. Knowing how memory is stored enables an advantage to a programmer. Since we know the L1 Cache is small (32 Kb) and an array is at most 32Kb (according to the graph above), if we iterate accordingly we should be able to fit an entire row of the matrix inside the cache at one time. At the maximum size of the matrix this is limited to a single row, meaning we can only store one row of the matrix at a time if each row is 32 Kb. This means that for the “poor cache optimization” the data in the L1 Cache is never accessed twice, requiring a request to either the L2, L3, RAM or the Hard Drive respectively. Since we know 32768 x 32768 * 4 bytes each (since they are integers) = 4 294 967 296 bytes or 4096 Mb or 4 Gb, we know that the L3 cache (with 8Mb) cannot store all of the data for the matrix and so it must go out to RAM many times to process the whole. This makes the “poor cache optimization” implementation some where around 10 times worse (40 L3 acces cycles / 4 L1 access cycles) than the “proper cache optimization” implementation.

Here are the average runtimes for the 32768 x 32768 matrices:

• Poor Implementation: 25.8573 seconds
• Proper Implementation: 2.76786 seconds
• “Supposed” Proper Implementation: 3.06805 seconds

The “Supposed” Proper Implementation is the function cache_opt is what you would be taught in a Computer Architecture or Systems Programming course, however in this case it does not actually have any better runtime. Why is this not the case? As stated before our processors currently prefetch for us, meaning… most of these issues are not really our issues any more. For example, the reason cache_opt should provide better results is because it breaks the 2D matrix into chunks which can be prefetched (meaning they are loaded into one of the caches before they are actually needed). However, because my processor automatically prefetches sequential information, it was roughly the same time as the “proper implementation.”

The importance of cache optimization seems clear at this point. A proper implementation of a for loop, being cache conscious can significantly speed up your program and in this case.

The data showed the proper implementation to be 9.34 times faster than the poor implementation.

This was very close to the earlier rough estimate where the poor implementation would be 10 times slower based on cache access times.

Data and Program:

• Google Sheet
• Github

Related

• Virtual Memory and You – How memory is actually stored/retrieved.
• The Cache and Multithreading – How to multithread with cache in mind.