The Newton Method
I kind of think of it as a song, “you put your P(z) in, you take your P'(z) out, you minus all from Zn and you get your Zn+1 out.” Alright, that might be a weak attempt to make an equation into song. Here’s the Newton Method equation (from Wikipedia):
Each time you calculate a new Zn+1 you plug it back into the equation until you find (within a small margin of error) the root of the equation p(z). Here is an image from wikipedia:
This is simple enough to do, however problems can occur if a horizontal asymptote is created by the p(z) or p'(z) equations. Therefore, we must keep that in mind whilst calculating/programming using newtons method.
Complex Numbers
To understand generates a fractal it is first required to understand the basics of complex numbers. Put simply a complex number is represented as the following, a + ib. Where ‘a’ represents a real number represented via our normal numerical representations and ‘b’ represents an imaginary number, not representable in the real world. Visually (picture taken from wikipedia):
Newton Fractals

Now that we have a rudimentary understanding of Newtons Method we would like to venture into the world of fractals. In essence a is a mathematical set that typically displays self-similar patterns, which means it is “the same from near as from far.” Or to paraphrase Benoit Mandelbrot:
Fractals are geometric objects with fractional dimensions rather than integer dimensions.
One of the ways we can display fractional dimensions is by using complex numbers. I’ll forgo the math at this point and leave the gory details for some later post. The following is an example of a fractal which should create a pretty picture, we use the following method:
- Given an equation F(Z), such as f(Z) = z^3 – 1, insert different pixel positions (x, y) into z = x + iy.
- Use Newtons method on Z to calculate the root for the given location
- Iterate over every pixel in the x by y image.
- If you pick an equation F(Z) with a given number of roots (such as 3) you can color each root a different color and make interesting pictures.
Here is the some python code to create some fractals, you can run this yourself on github (but not on OSX):
Output:
Function: z^3 – 1
Function: z^2 – 2z + 2
Function: z^6 – z^3 + 2
Function: z^3 – 2z + 2
Function: z^5 – z

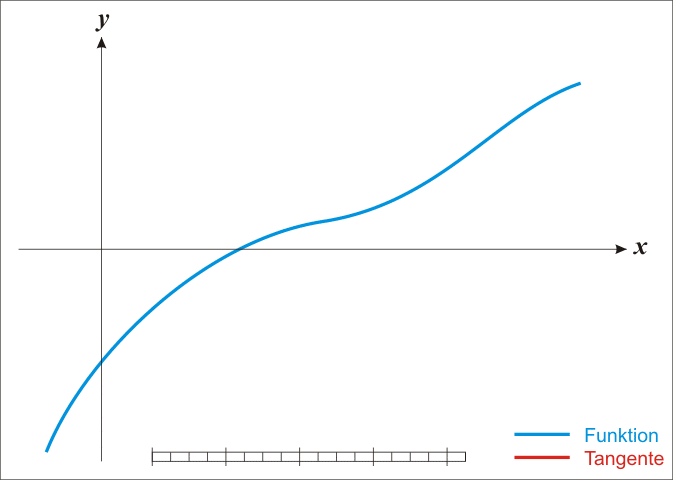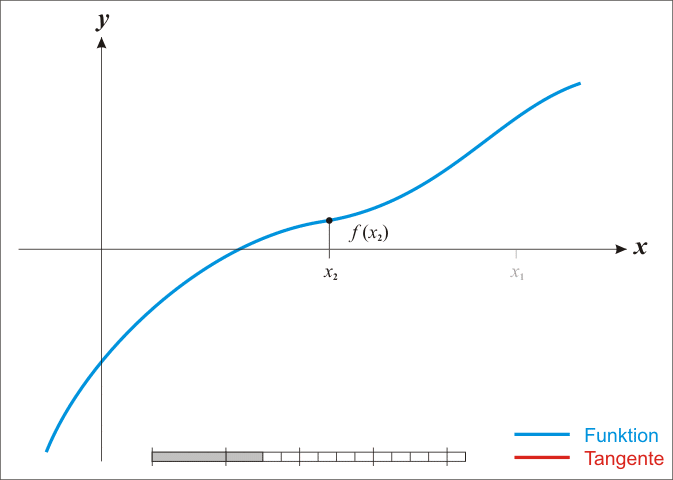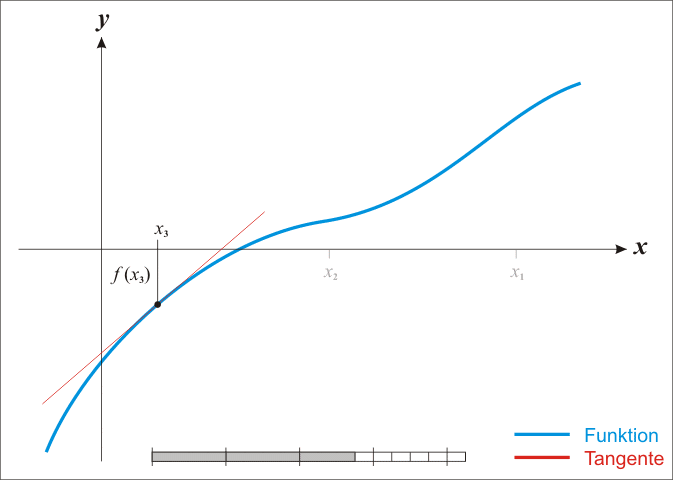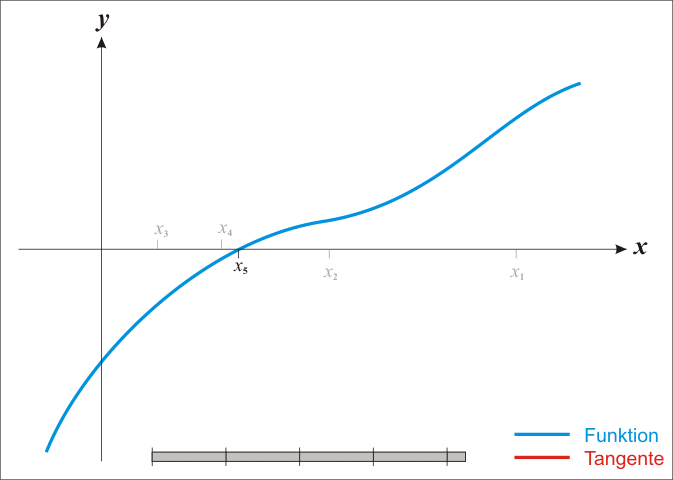





He blogs, he writes songs, he bathes hairless cats (or at least he will) — what can’t Austin do? I was going to make a very clever comment about Newton’s method being “just binary search,” but the more I think about it, the more confused I become. Such is life.
It is very similar to binary search, however there is not a guarantee of convergence. Meaning it could take an infinitely long time to converge, as opposed to O(logN) worst case runtime for binary search. Further, because you can potentially have a function which produces a VERY squiggly line making it take a VERY long time for convergence.
The Weierstrass function comes to mind — “I recoil with fear and loathing from that deplorable evil, continuous functions with no derivative.”