The Problem
According to Wikipedia the Dinning Philosophers Problem is described as follows:
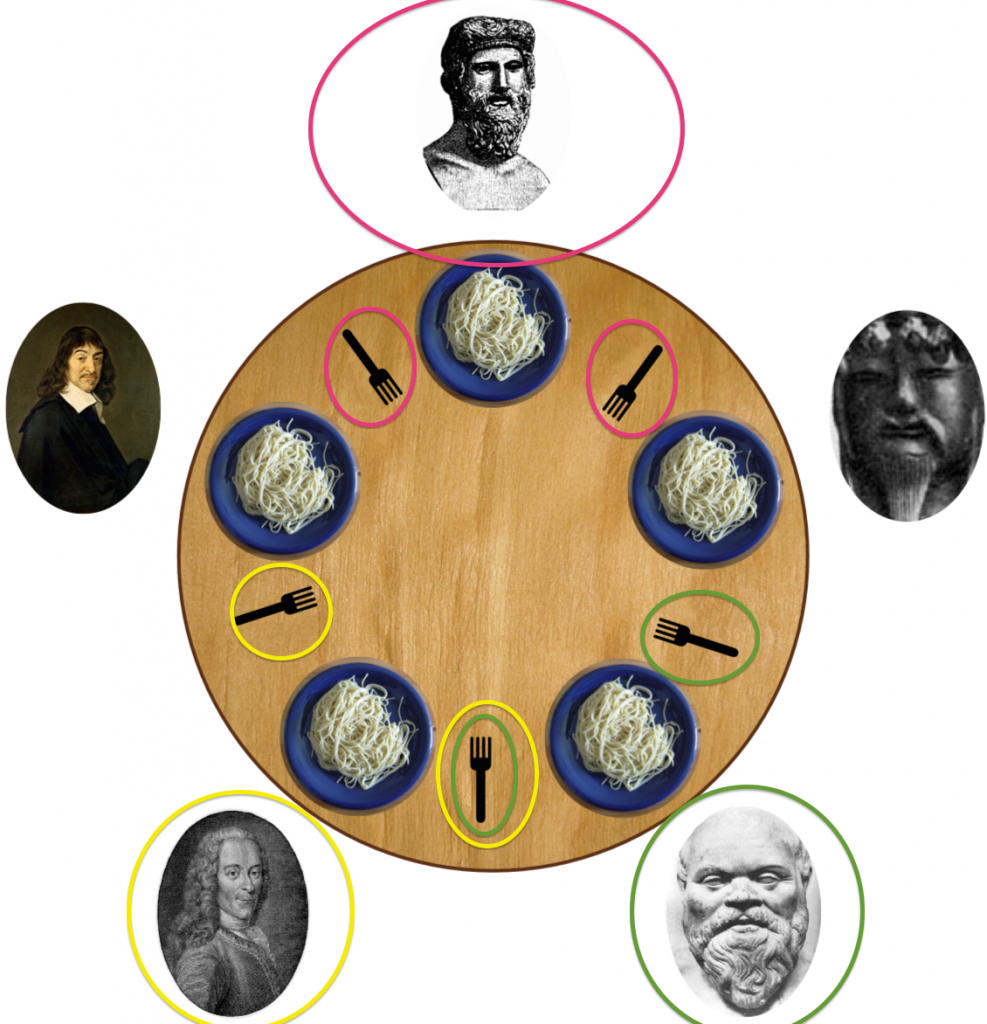
Five silent philosophers sit at a table around a bowl of spaghetti. A fork is placed between each pair of adjacent philosophers. (An alternative problem formulation uses rice and chopsticks instead of spaghetti and forks.)
Each philosopher must alternately think and eat. However, a philosopher can only eat spaghetti when he has both left and right forks. Each fork can be held by only one philosopher and so a philosopher can use the fork only if it’s not being used by another philosopher. After he finishes eating, he needs to put down both forks so they become available to others. A philosopher can grab the fork on his right or the one on his left as they become available, but can’t start eating before getting both of them.
Eating is not limited by the amount of spaghetti left: assume an infinite supply.
The problem is how to design a discipline of behavior (a concurrent algorithm) such that each philosopher won’t starve; i.e., can forever continue to alternate between eating and thinking assuming that any philosopher cannot know when others may want to eat or think.
In other words we start with this:
Then try to go to this:
Now, if we are trying to multithread this requires a fair amount of finesse. It’s not possible to simply say, “EAT” and everyone eats. If we did try to have each philosopher grab the fork on his right and never give it up we would end up with something called a deadlock. In other words, the process would be stuck and there would be no way for any philosopher to eat their spaghetti since in this problem, each philosopher needs both forks (since apparently these philosophers are a bit odd).
In multithreaded processes this is a standard and fairly difficult problem (for beginners), and we need some sort of algorithm to ensure each philosopher can eat all the food on his plate.
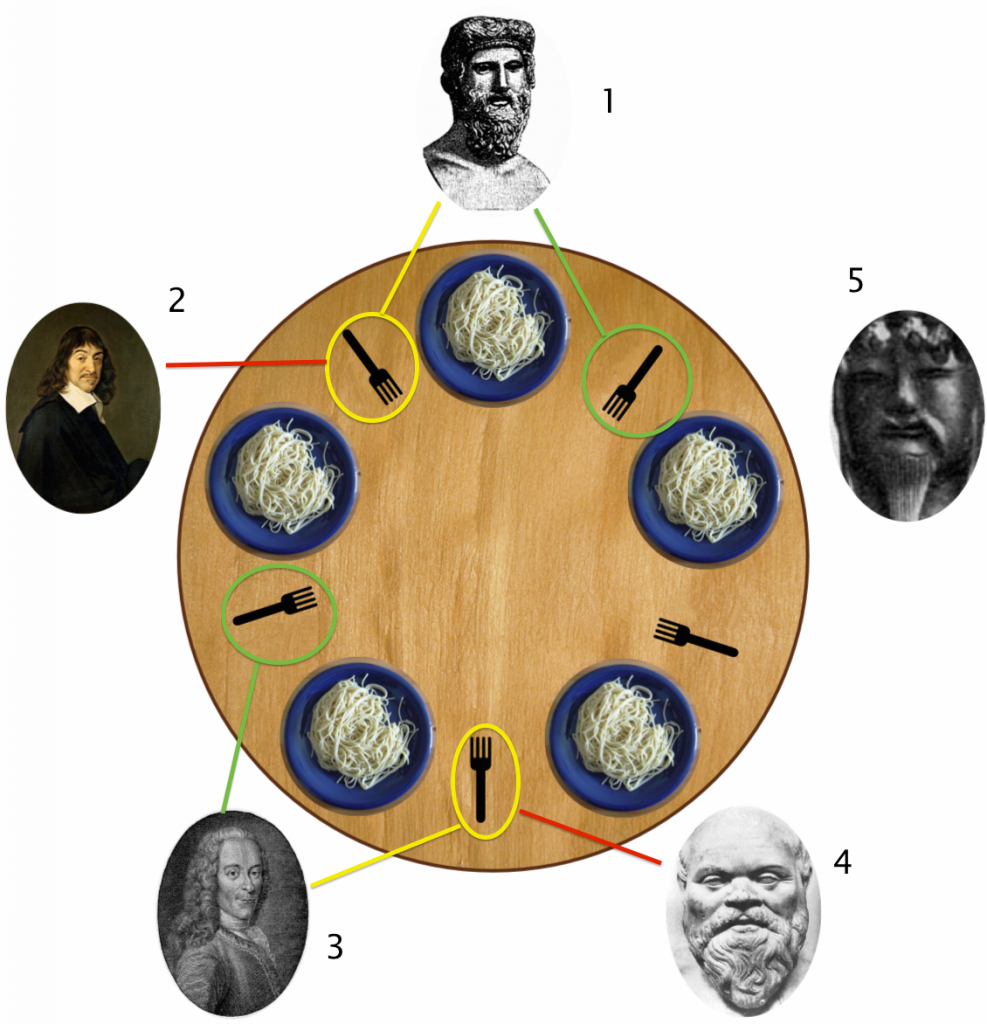
Solution #1 – King of the Table
One fairly easy solution is to simply make a “king” for each table who is the only philosopher who can eat. This is a pretty poor solution, take the following:
If in the image above only one philosopher is able to eat at a time and in this picture he is the philosopher with the red circles. We are then leaving the philosophers with either yellow or green circles sitting there doing no work when there is no reason one of them cannot be eating. Although this solution avoids any deadlocks it is inefficient and not worth implementation.
Solution #2 – Waiter may I?
In this solution we can simply have a user input or have a pre-defined order in which the philosophers can eat, in either case a mutex would be needed. If we number the philosophers as 1, 2, 3, 4, 5 and we simply use an array which is in shared memory between threads we can ensure that no philosophers adjacent to one another have access to eat at once. Example: Philosophers 1 and 3 can eat, but 2 and 3 cannot try to eat at the same time. This is a relatively straight forward, easiest, but least general solution.
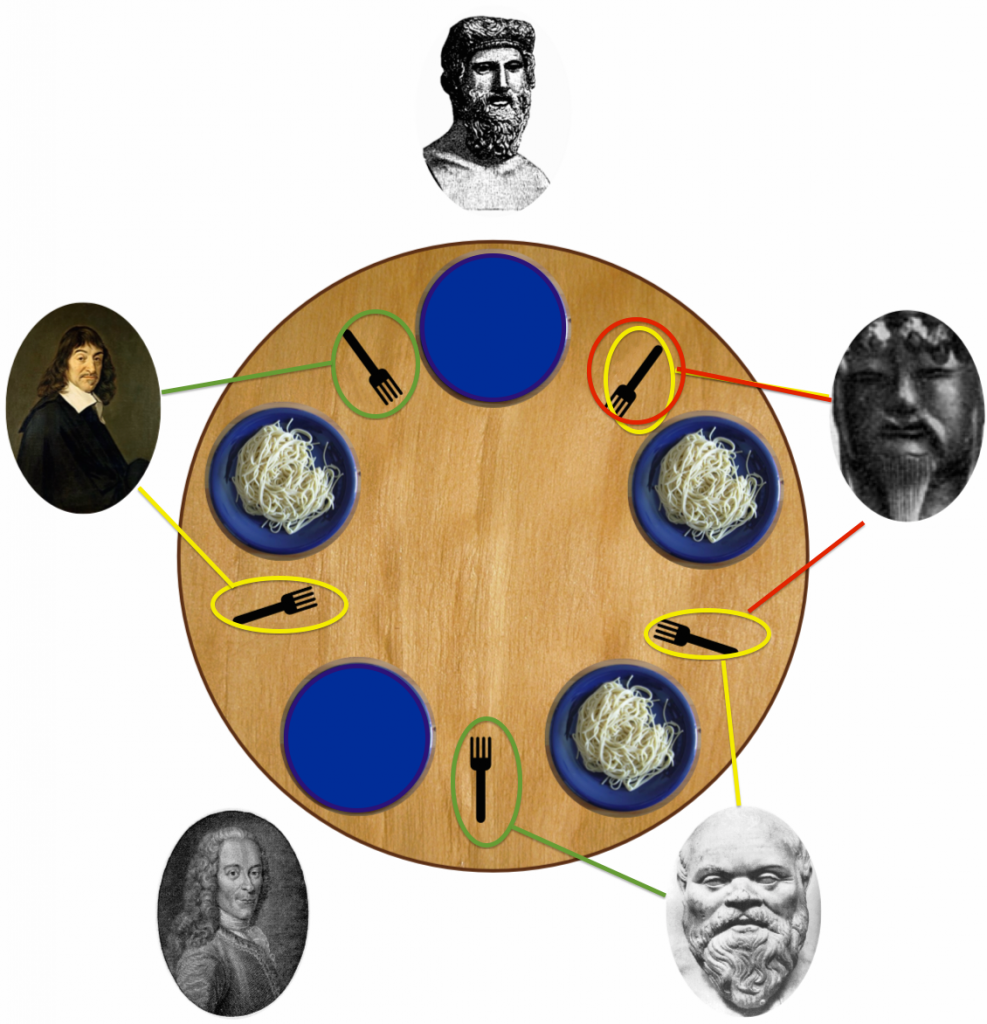
Solution #3 – Right, then Left or Release
In this solution we do the following:
To initialize the philosophers eating we do the following:
- Number/identify each philosopher
- Initialize [a] semaphore(s) to ensure each philosopher gets an opportunity to eat.
- Going clockwise around the table each philosopher pick up the fork to his right
- Then, going counter-clockwise around the table have the philosophers try to grab the forks to their left.
- If it is unavailable (s)he releases the right fork and waits.
- Iterate again going clockwise and each philosopher who has access to his left and right fork pick both up.
We can then simply rotate clockwise one position every new “turn” of eating. This is superior to the solution #2 because it is generalized and the number of philosophers need not be known.
This however is not a very efficient solution, although it does prevent deadlocks it requires 2*n iterations (n being the number of philosophers) to initialize the “turn” eating. The images below are a visual representation of the algorithm:
- Number/identify each philosopher
- Store a “count” for each philosopher
- Going clockwise around the table each philosopher pick up the fork to his right
- Then, going counter-clockwise around the table have the philosophers try to grab the forks to their left.
- If it is unavailable (s)he releases the right fork and waits.
- Iterate again going clockwise and each philosopher who has access to his left and right fork pick both up.
- Rotate clockwise one position every new “turn” of eating.
As you can see philosopher 5 still has to wait to eat, but the following turn he and philosopher 3 will have access to their forks. Alternatively, you could rank each of the forks and use more or less the same method.
Solution #4 – Chandy/Misra
This was taken from wikipedia solutions to this problem and “technically” breaks the rules since the philosophers are communicating:
- For every pair of philosophers contending for a resource, create a fork and give it to the philosopher with the lower ID. Each fork can either be dirty or clean. Initially, all forks are dirty.
- When a philosopher wants to use a set of resources (i.e. eat), he must obtain the forks from his contending neighbors. For all such forks he does not have, he sends a request message.
- When a philosopher with a fork receives a request message, he keeps the fork if it is clean, but gives it up when it is dirty. If he sends the fork over, he cleans the fork before doing so.
- After a philosopher is done eating, all his forks become dirty. If another philosopher had previously requested one of the forks, he cleans the fork and sends it.
Summary
This problem is often used to explain how deadlocks are formed, and how to avoid and solve such problems. These are often difficult to solve for a novice programmer, so do not get discouraged. It’s fairly easy to make a mistake when dealing with multithreading and it takes time to understand how all of the threads interact.