Radix Sort is a relatively old being discovered in 1887 by Herman Hollerith, and it is a non-comparitive integer sorting algorithm. In many ways Radix Sort in C is an extension of Counting Sort in C, which I recommend reviewing as well, as it will provide must of the background for Radix Sort.
Radix Sort
The algorithm follows the following pattern:
- Receive an unsorted array of integers, often referred/represent a key.
- Iterate from most to least (or least to most) significant digits.
- Each iteration sort all of the values of the current significant digit the array.
* A key in this case, is an integer value, which can be associated with other data, such as birth date, location, etc.
To demonstrate, we will complete an example problem with four integers to sort:
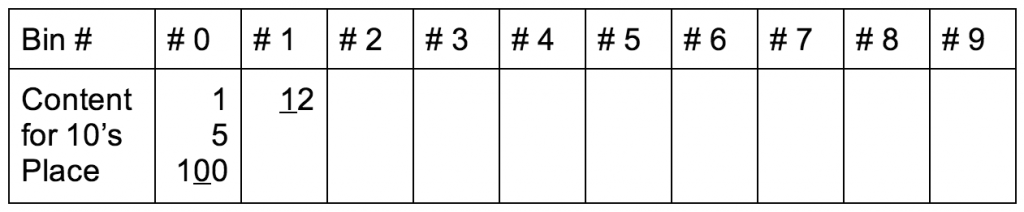
Original: 100, 12, 1, 5
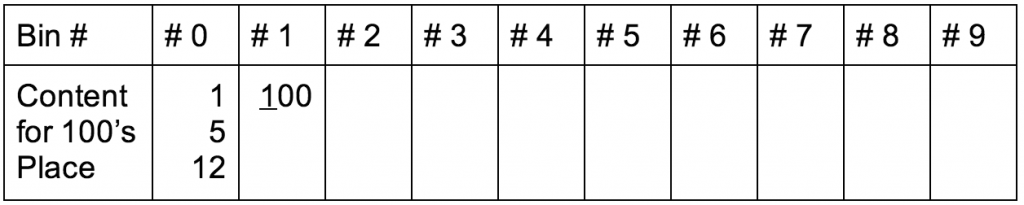
{ 100, 12, 1, 5 } -> { 100, 1, 12, 5 }
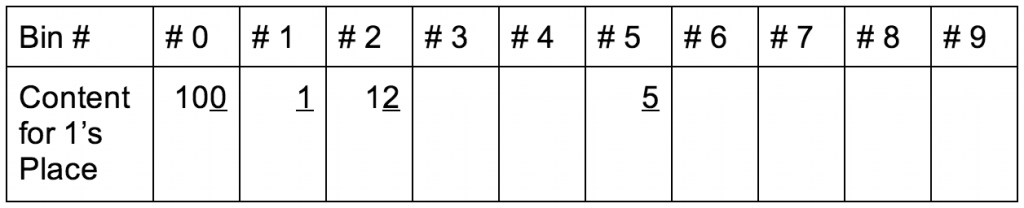
{ 100, 1, 12, 5 } -> { 1, 5, 100, 12 }
{ 1, 5, 100, 12 } -> { 1, 5, 12, 100 }
Sorted: 1, 5, 12, 100
Notice, if you watch the “100” through various iterations, you’ll see it is simply move one significant digit to the left and we sort by that digit or 10’s place. It is also possible to go left to right, i.e. most significant digit to least significant digit, but this is the more common method.
Example by Hand
Implementing this algorithm requires a bit more handy work than I let on. First, let me make it clear that there are several ways to implement Radix Sort in C (or out of C), and this is not a clearly defined “correct” method. In order to efficiently implement Radix Sort, we use something called “buckets” which will store the index of the sorted significant digits, similar to Counting Sort.
For example, the bucket for iteration one would be as follows:
Note: bucket[index to array position]
array[100, 1, 12, 5] -> bucket[0, 1, 2, 2, 2, 3, 3, 3, 3, 3]
The reason for the repeated numbers is because we have a value of 0, 1, 2, and 5 for the value at the given significant digit (in this case the 1’s place). The implementation I am using adds a number to the bucket[index] when ever there is a new value for a given significant digit.
If we then added the number 101 to the list, we would have the following bucket:
array[100, 101, 1, 12, 5] -> bucket[ 0, 1, 3, 3, 3, 4, 4, 4, 4, 4]
Notice, the orange 2 has changed to a orange 3, this is because the new 2-value bucket starts at 3rd position in the semi-sorted array.
Now let’s add the number 8 to the list, we will have the following bucket:
array[100, 101, 1, 12, 5, 8] -> bucket[0, 1, 3, 3, 3, 4, 4, 4, 5, 5]
Reflect that 8 is the 5th index in the sorted significant digit array, represented with the number 5 in the 8th index/position in the bucket array.
- Time: O(nk), where n is the number of elements and k is the number of bits per element
- Space: O(n + k), where n is the number of elements and k is the number of bits per element
Code | Radix Sort in C Algorithm
Feel free to fork the following code on Github
Output:
Running Radix Sort Example in C!
———————————-
Unsorted List: [10 2 303 4021 293 1 0 429 480 92 2999 14]
Running Radix Sort on Unsorted List
Sorting: 1’s place [10 2 303 4021 293 1 0 429 480 92 2999 14]
Bucket: [0 3 5 7 9 10 10 10 10 10]
Sorting: 10’s place [10 0 480 4021 1 2 92 303 293 14 429 2999]
Bucket: [0 4 6 8 8 8 8 8 8 9]
Sorting: 100’s place [0 1 2 303 10 14 4021 429 480 92 293 2999]
Bucket: [0 7 7 8 9 11 11 11 11 11]
Sorting: 1000’s place [0 1 2 10 14 4021 92 293 303 429 480 2999]
Bucket: [0 10 10 11 11 12 12 12 12 12]
Sorted List: [0 1 2 10 14 92 293 303 429 480 2999 4021]
You can also review my Go implementation: Radix Sort in Go, the numbers are the same!
Summary
Due to its reliance on memory and the requirement of fixed-length integer keys, this algorithm is often overlooked or unused (reasonably so). There are several applications of Radix Sort which can be useful, such as parallel computing, but Radix Sort is not really a “general purpose” or “everyday use” sorting algorithm. For the average or more general use case quicksort or merge sort is probably a safer bet. If you are still interested I recommend reading further discussion on stack exchange and stack overflow.
Related Articles
- Introduction to Markov Processes (a.k.a. Markov Chains)
- Using SVD to Obtain Regression Lines
- Everyday Algorithms: Pancake Sort
- I/O Multiplexing using epoll and kqueue System Calls
- Intro to IPC | Interprocess Communication
Recommended Books
- This question is often on interview questions, and I recommend: Cracking the Coding Interview: 150 Programming Questions and Solutions if that is what brought you here.
- If you are here for a class or just because you enjoy algorithms, my favorite algorithms book (thus far) has been: Introduction to Algorithms (Cormen, Leiserson, Rivest, Stein).
- A close second for algorithms is Jeff Erickson’s Algorithms, which is really more of a collection of notes (but it’s free!).