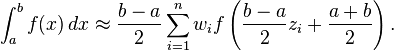Gaussian Quadrature can be used to approximate an integral, I have done a comparison on different quadrature methods previously. However, I will not be comparing Gaussian Quadrature (for the moment), instead I will be going over how it works and why it is an excellent approximation of integrals.
Gaussian Quadrature
Formally it is defined as,
However, I prefer to think of it as,
In essence, the way Gaussian Quadrature is used is similar to the Trapezoidal or Simpson’s method, however instead of using fixed points, we use varying points as well as weights (wi). This allows for a much more accurate approximation of an integral, so much so that it seems silly to even compare the methods of quadrature I compared earlier.
Example
I know I always learn better with an example, so here it goes:
Clear this method is excellent in both accuracy and computational complexity. The number of calculations required are O(1) given the number of steps. Further, we can look up the weights and points in a table which makes it even quicker. This is by far better than the methods previous compared, and I would suggest everyone use it to approximate integrals.
Related Articles
Useful Resources:
- Lagradre-Gauss Quadrature (wolfram.com)
- [Video] Gauss Quadrature Rule: Two Point Rule (youtube.com)
- Gauss Quadrature (pomax.github.io)